Notes on Zippers (in Haskell)

I'm trying to implement the triangle "tree" (it's really more of a DAG) from the Faniry-AIMS paper on Delaunay triangulation¹, and I want to do it as a zipper.

If you want to see how this "discussion" evolves, see it in GitHub @ https://github.com/JohnL4/Tarheel-NC/blob/master/Haskell/zippers.org.

For more info on zippers, see http://learnyouahaskell.com/zippers (there are lots of other references to Haskell zippers on the web, but they all seem to be trees, which is great, but I've got a weird DAG, so I'm kinda sorta on my own).

There's also this interesting article: http://blog.ezyang.com/2010/04/you-could-have-invented-zippers/.

And:

• http://www.sciencedirect.com/science/article/pii/S1571066106001289 (via https://stackoverflow.com/questions/46400446/immutable-functional-data-structure-to-represent-graphs)
• https://stackoverflow.com/questions/9732084/how-do-you-represent-a-graph-in-haskell (which I've seen before, but coming back to it, i realize it's probably pretty decent)

Anyway, here's the tree structure, in more-or-less abstract terms:

-- | A dumb daggy tree.
data TriTree = TriTree {
  triangle :: Set Point,   -- ^ Exactly 3 points -- We use sets so we can use intersections to see if two triangles are
                           -- neighbors.
  isOld :: Bool,           -- ^ Whether or not this triangle is old.
  kids :: Set TriTree,     -- ^ 0, 2, or 3 kids
  parents :: Set TriTree,  -- ^ 1+ parents (this node should be in parent's set of kids)sort?
  neighbors :: Set TriTree -- ^ 0-3 neighbors (is it possible for a triangle to have one neighbor?).  Note that it is
                           -- not necessarily the case that a triangle's neighbors are its siblings in the tree
                           -- structure.
  }
  deriving (Eq, Ord, Show)

The data each node carries is a triangle (3 points) and a Boolean "is old" flag. The triangle never changes but the Boolean gets flipped once from false to true in the course of operating on the tree.

Each tree node has children, which are more triangles. I'm pretty sure there are only two or three children (or zero, if it's a leaf node).

Each triangle also has "neighbors", the adjacent triangles. A triangle has three sides, so it'll have three neighbors, at most. (This is a triangular mesh, so there's nothing tricky with two different triangles each sharing half the edge of an adjacent triangle.)

And, finally, because of the algorithm, we start out with a tree structure (each node having at most one parent) but we pretty quickly introduce extra parents at various nodes, so each node can have more than one parent. All parents lead to the root, though.

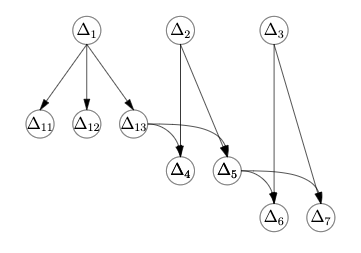
Here's a sample tree, stolen right out of the paper:

In this diagram, the root isn't shown, but it's the parent of triangles 1, 2, and 3. As you can see, triangles 4, 5, 6, and 7 all have multiple parents.

I dunno, waddya lookin' at me for?

I think the idea is that it's like a zipper on a piece of clothing (say, a jacket). It can be half unzipped, and you can pick it up by the handle and get the whole zipper, but you're not holding it by one end, but by something in the middle.

Also, the zipper splits and joins the data structure as you slide it up and down, like a real zipper does.

Maybe you could also think of it as sort of a cursor that can be used to refer to the entire data structure, and that can be used to point to different parts of the data structure as you "make changes" to the data structure.

So, wherever we are, we need to be able to completely reconstruct the tree. Part of the reason we're doing this is so we can effect state changes in the tree. Since this is Haskell, obviously, we can't just "effect state changes". Instead, we have to return a new data structure, a copy with our changes in it. So, we move the zipper to a node, and plug in a new node having the same references to the kids, neighbors and parents.

Normally, for a plain tree, we don't need to maintain parent pointers, but in this case, I think we need to maintain at least sets of "extra parent" links.

So, the zipper is:

• current node value (triangle, Boolean), including children and neighbors (what if we navigated from a neighbor?)